Contents Previous Next

Functions

A function 𝕗 which takes a value of type 𝔸 and returns a value of type 𝔹, is said to be of type 𝔸 → 𝔹 and is written as 𝕗 : 𝔸 → 𝔹. The type 𝔸 is called the function 𝕗’s “domain” and 𝔹 is the “co-domain”.

{-# OPTIONS --allow-unsolved-metas #-}

module Lang.functions where

open import Lang.dataStructures hiding (_+_)

Generic Syntax

Syntax for defining functions in Agda:

  1. Define name and type of function
  2. Define clauses for each applicable pattern
-- 1. Name (not), Type (Bool → Bool)
not : Bool → Bool
-- 2. Clause 1: if the argument to `not` is `true`
not true = false
-- 2. Clause 2: if the argument to `not` is `false`
not false = true

Examples - Pattern matching functions

The Logical Not

The simplest of functions simply match patterns. For example the function for not:

not : Bool → Bool
not true = false -- return false if we are given a true
not false = true -- return a true if we are given a false

we could also use a wildcard type (_) like this:

not₁ : Bool → Bool
not₁ true = false -- return false if we are given a true
not₁ _ = true -- return true in all other cases

The logical AND

In Agda, function names containing _s indicate those functions can behave as operators. Hence _+_ indicates that instead of calling the functions +(a, b) one can call it as a + b, whereas if_then_else_ can be called as if condition then 2 else 3.

One has to also define whether the infix operator is left or right associative (infixl, infixr) and its precedence level. The default precedence level for a newly defined operator is 20.

_∧_ : Bool → Bool → Bool
true ∧ whatever = whatever -- true AND whatever is whatever
false ∧ whatever = false -- false AND whatever is false

infixr 6 _∧_

The logical OR

_∨_ : Bool → Bool → Bool
true ∨ whatever = true -- true or whatever is true
false ∨ whatever = whatever -- false or whatever is whatever

infixr 6 _∨_

These functions can be applied as:

notTrue : Bool
notTrue = not true

false₁ : Bool
false₁ = true ∧ false

true₁ : Bool
true₁ = true ∨ false ∨ false₁

Examples - Recursive functions

Addition of natural numbers

Here we follow a similar pattern as in data, we define:

_+_ : ℕ → ℕ → ℕ
zero + n = n
succ m + n = succ (m + n)

infixl 6 _+_

Thus, we can use them to get new numbers easily:

eleven = ten + one
twelve = eleven + one
thirteen = twelve + one

Length of a List

The length of a list consists of traversing through the list and adding one for each element:

length : List ⊤ → ℕ
length [] = zero
length (x :: xs) = one + (length xs)

Dependent Function Types or Π-types

Dependent pair types are a pair of two types such that the second type is a function of the first type:

data Σ (A : Set) (B : A → Set) : Set where
  _,_ : (a : A) → (b : B a) → Σ A B

Similar to dependent pair types, a dependent function type is a function type whose result type depends upon its argument value. The notation in type theory looks like this for binary dependent function types:

\[ \prod_{x : A} B(x) \]

with ternary dependent pair types being represented as:

\[ \prod_{x : A} \prod_{y : B(x)} C(y) \]

and so on.

Lambda Functions

Lambda or anonymous functions can be defined using the following syntax:

example₁ = \ (A : Set)(x : A) → x

and a more concise syntax:

example₂ = λ A x → x

Note that \ and λ can be used interchangeably.

Following are a few examples of functions:

Examples of further patterns

Implicit Arguments: List concatenation

Functions in Agda can work with implicit parameters. For example, instead of having the specify the type of A, the compiler can be expected to figure it out. Hence instead of defining _++_ : (A : Set) → List A → List A → List A, we define it like:

_++_ : {A : Set} → List A → List A → List A
[]        ++ ys = ys
(x :: xs) ++ ys = x :: (xs ++ ys)

infixr 5 _++_

Note that the curly braces {} are “implicit arguments” in Agda. Values of implicit arguments are derived from other arguments’ (in this case List A) values and types by solving type equations. You don’t have to apply them or pattern match on them explicitly (though they can be explicitly passed like function_name{A = A}).

This function takes a type as a parameter A, and hence can work on Lists of any type A. This feature of functions is called “parametric polymorphism”.

Dot patterns: Square

A dot pattern (also called inaccessible pattern) can be used when the only type-correct value of the argument is determined by the patterns given for the other arguments. The syntax for a dot pattern is .t.

As an example, consider the datatype Square defined as follows:

data Square : ℕ → Set where
  sq : (m : ℕ) → Square (m × m)

Suppose we want to define a function root : (n : ℕ) → Square n → ℕ that takes as its arguments a number n and a proof that it is a square, and returns the square root of that number. We can do so as follows:

root : (n : ℕ) → Square n → ℕ
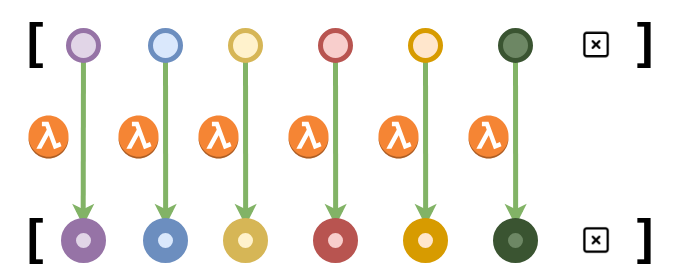
root .(m × m) (sq m) = m

Map

We implement the map function, of “map-reduce” fame, for Lists: A map function for a List is a function that applies a lambda (un-named) function to all elements of a List.

If f were a lambda function, map-ing f over List(a, b, c, d) would produce List(f(a), f(b), f(c), f(d))

Figure 1: Map 
map : {A B : Set} → List A → (A → B) → List B
map [] f = []
map (x :: xs) f = (f x) :: (map xs f)

Here, we apply the function addOne to a list, using map:

addOne : ℕ → ℕ
addOne x  = x + one

oneAdded : List ℕ
oneAdded = map (one :: two :: three :: four :: []) addOne

Syntactical Sugar

prop₁ : ((x : A) (y : B) → C) is-the-same-as   ((x : A) → (y : B) → C)
prop₂ : ((x y : A) → C)       is-the-same-as   ((x : A)(y : A) → C)
prop₃ : (forall (x : A) → C)  is-the-same-as   ((x : A) → C)
prop₄ : (forall x → C)        is-the-same-as   ((x : _) → C)
prop₅ : (forall x y → C)      is-the-same-as   (forall x → forall y → C)
(\x y → e)                    is-the-same-as   (\x → (\y → e))
(f a b)                       is-the-same-as   ((f a) b)

Modules, Records and Postulates