Contents Previous Next

Algebraic Topology

module AlgTopos.introduction where

The field of Topology studies the properties of objects that are preserved under continuous deformations, such as stretching, twisting, crumpling and bending, but not tearing or gluing. The main object of study is called a “Topological Space” and the deformations “Homeomorphism”s. Generally well-known geometric objects such as metric spaces (like the 3-D real space we live in and all objects we have ever experienced) are all examples of topological spaces. The branch of Algebraic Topology is the study of the properties of topological spaces and continuous maps or Homeomorphisms between them using the tools of abstract algebra.

Here we present the most familiar of examples of Homeomorphisms: that a coffee mug and a donut are topologically the same object (are Homeomorphic).

Figure 1: Homeomorphism

The primary properties of spaces studied include:

  1. Homotopy
  2. Homology
  3. Cohomology

These properties also help in classifying the spaces into various types.

Algebraic Topology also includes in-depth studies of special kinds of spaces, major ones being:

  1. Manifolds
Figure 2: The Calabi-Yau manifold
  1. Knots
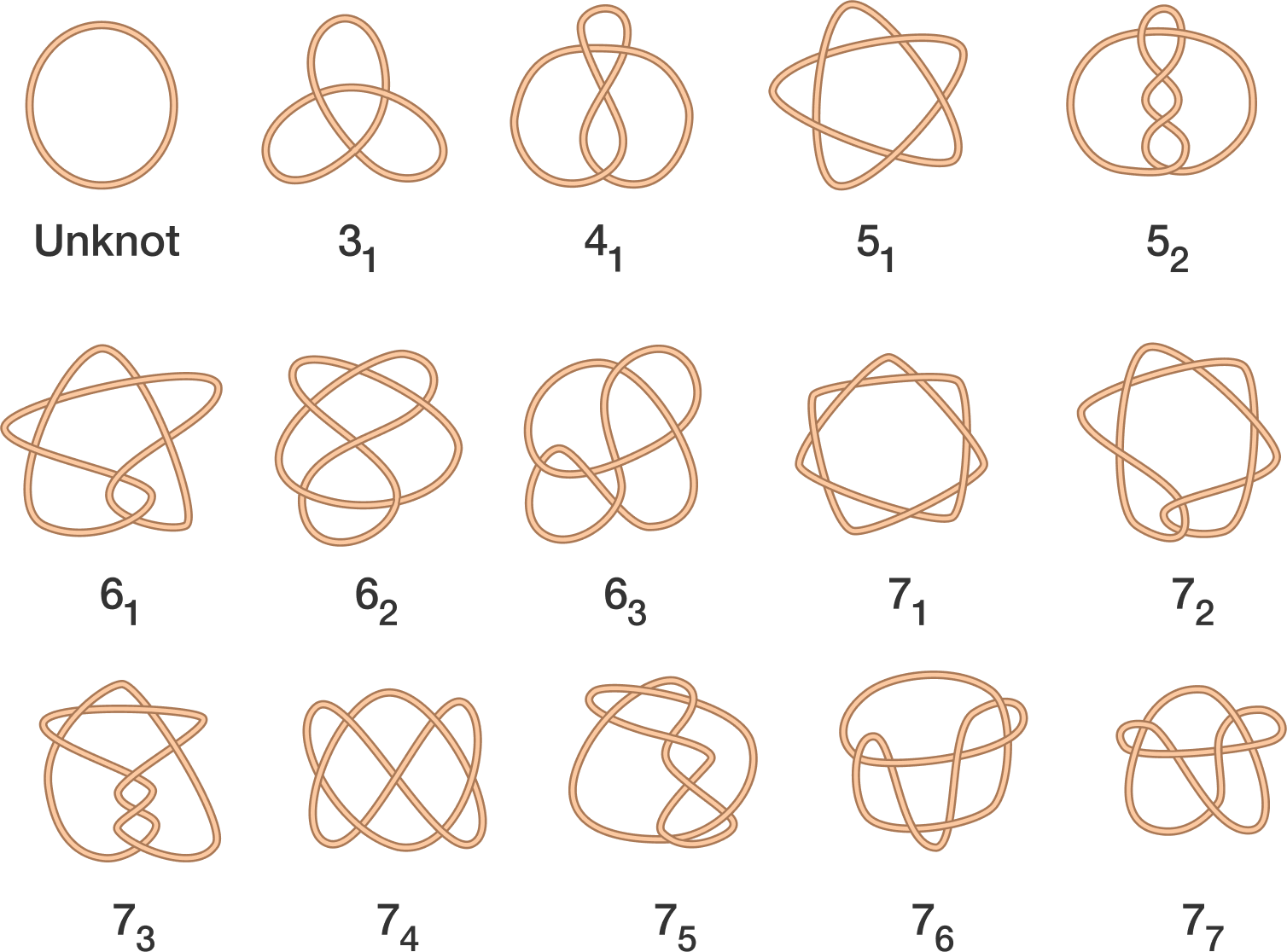
Figure 3: Knots
  1. Simplical Complexes
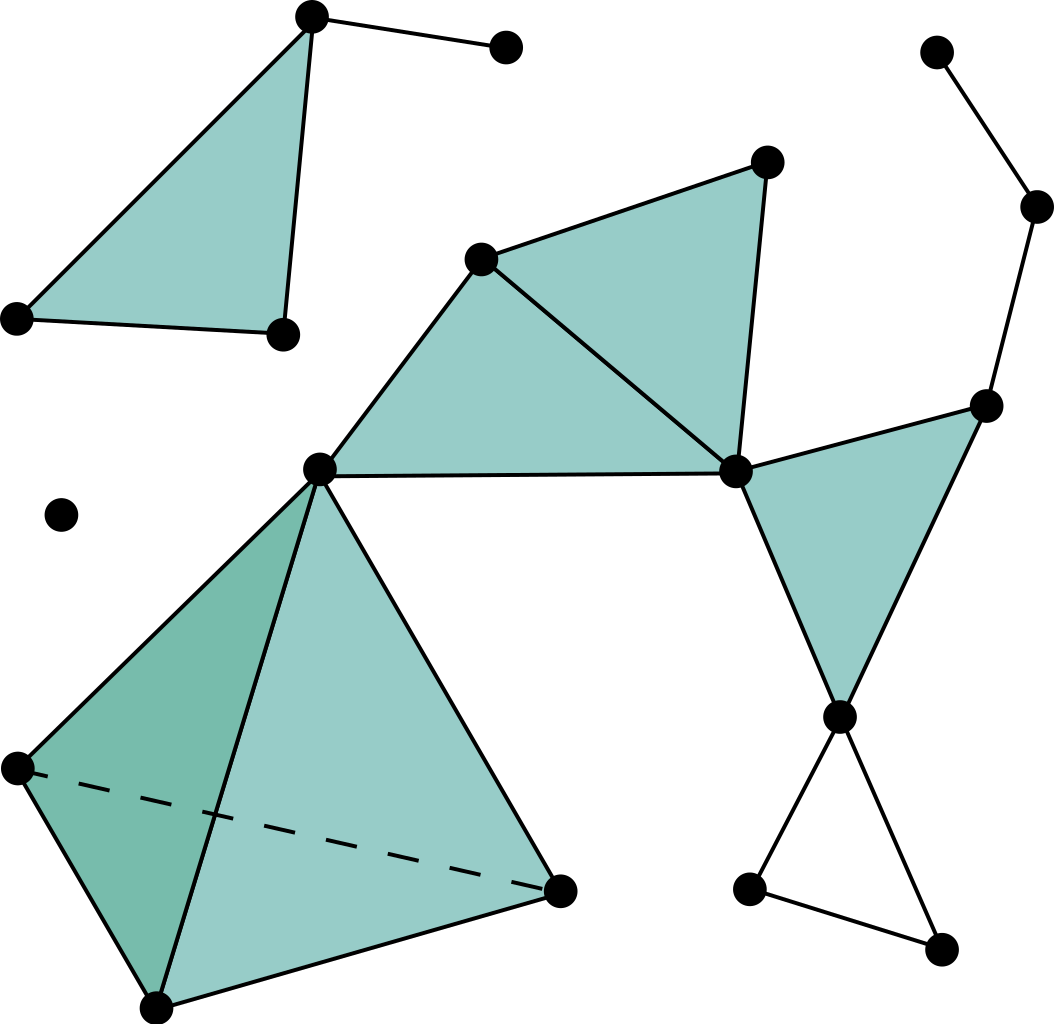
Figure 4: Simplical Complex

We first start with basics of topology where we see what we exactly mean by Topological Spaces, Homeomorphisms and Homotopies. We then take a look at applying algebraic structures to studying Topology and try to cover some important concepts.

Spaces and Paths