Contents Previous Next

Morphisms

module Algebra.groupMorphisms where

open import Agda.Primitive using (Level; _βŠ”_; lsuc; lzero)
open import Types.relations
open import Types.equality
open import Types.functions2

open import Algebra.groups
open import Algebra.groups2

A morphism is a more general concept that applies not only to groups but also to pretty much all algebraic objects. It can be defined as a structure-preserving map. In the context of group-like objects, a morphism between any two objects X and Y embeds X in Y while ensuring the structure of X is preserved.

Let us first define a morphism:

module Homomorphism {f t β„“} (From : Set f) (To : Set t) (_==_ : Rel To β„“) where
  Morphism : Set _
  Morphism = From β†’ To

In the family of groups, these are the main kinds of morphisms:

  1. Homomorphism
  2. Endomorphism
  3. Isomorphism
  4. Automorphism

Homomorphisms

A map (function) 𝔽 is a homomorphism if given input x ∈ (X, β€’), where X is a group-like structure, its output y ∈ (Y, ∘) where Y is also a group-like structure, such that 𝔽 preserves the group-like structure of X in Y, i.e.Β it ensures that all relations what were valid in X remain valid in Y. More formally,

Given two groups, (X, β€’) and (Y, ∘), 𝔽 : X β†’ Y is a homomorphism if:

\[ βˆ€ x₁, xβ‚‚ ∈ X, π”½βŸ¦ x₁ β€’ xβ‚‚ ⟧ = π”½βŸ¦ x₁ ⟧ ∘ π”½βŸ¦ xβ‚‚ ⟧ \]

The basic rules for any morphism to be a homomorphism are if it:

  1. Preserves identity

An identity homomorphism when applied to a structure produces the same structure.

  identity-preservation : Morphism β†’ From β†’ To β†’ Set _
  identity-preservation π•„βŸ¦_⟧ from to = π•„βŸ¦ from ⟧ == to
  1. Composes with operations

If 𝔽 is a homomorphism from X β†’ Y, and β‹… and ∘ are both unary or both binary operations operating on X and Y respectively, then 𝔽 composes with the two operations in the following ways:

  compose-unary : Morphism β†’ β™  From β†’ β™  To β†’ Set _
  compose-unary π•„βŸ¦_⟧ βˆ™_ ∘_ = βˆ€ x β†’ π•„βŸ¦ βˆ™ x ⟧ == ( ∘ π•„βŸ¦ x ⟧ )

  compose-binary : Morphism β†’ β˜… From β†’ β˜… To β†’ Set _
  compose-binary π•„βŸ¦_⟧ _βˆ™_ _∘_ = βˆ€ x y β†’ π•„βŸ¦ x βˆ™ y ⟧ == ( π•„βŸ¦ x ⟧ ∘ π•„βŸ¦ y ⟧ )

Now, we define homomorphisms for various group-like structures we have discussed earlier.

Magma homomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Magma f ℓ₁) (To : Magma t β„“β‚‚) where
  private
    module F = Magma From
    module T = Magma To

  open Homomorphism F.Data T.Data T._==_

  record IsMagmaHomomorphism (π•„βŸ¦_⟧ : Morphism) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      preserves-congruence    : π•„βŸ¦_⟧ Preserves F._==_ ⟢ T._==_
      preserves-composition   : compose-binary π•„βŸ¦_⟧ F._βˆ™_ T._βˆ™_

Semigroup homomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Semigroup f ℓ₁) (To : Semigroup t β„“β‚‚) where
  private
    module F = Semigroup From
    module T = Semigroup To

  open Homomorphism F.Data T.Data T._==_

  record IsSemigroupHomomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-magma-homomorphism  : IsMagmaHomomorphism F.magma T.magma π•„βŸ¦_⟧

    open IsMagmaHomomorphism is-magma-homomorphism public

Monoid Homomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Monoid f ℓ₁) (To : Monoid t β„“β‚‚) where
  private
    module F = Monoid From
    module T = Monoid To

  open Homomorphism F.Data T.Data T._==_

  record IsMonoidHomomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-semigroup-homomorphism  : IsSemigroupHomomorphism F.semigroup T.semigroup π•„βŸ¦_⟧
      preserves-identity         : identity-preservation π•„βŸ¦_⟧ F.Ξ΅ T.Ξ΅

    open IsSemigroupHomomorphism is-semigroup-homomorphism public

Group Homomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Group f ℓ₁) (To : Group t β„“β‚‚) where
  private
    module F = Group From
    module T = Group To

  open Homomorphism F.Data T.Data T._==_

  record IsGroupHomomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-monoid-homomorphism  : IsMonoidHomomorphism F.monoid T.monoid π•„βŸ¦_⟧
      preserves-inverse       : compose-unary π•„βŸ¦_⟧ F._⁻¹ T._⁻¹

    open IsMonoidHomomorphism is-monoid-homomorphism public

Automorphism

An Automorphism is a homomorphism between the object to itself.

Monoid automorphism

module _ {f β„“} (Self : Monoid f β„“) where
  private
    module S = Monoid Self

  open Homomorphism S.Data S.Data S._==_

  record IsMonoidAutomorphism (π•„βŸ¦_⟧ : Morphism) : Set (f βŠ” β„“) where
    field
      is-homomorphism : IsMonoidHomomorphism Self Self π•„βŸ¦_⟧

Group automorphism

module _ {f β„“} (Self : Group f β„“) where
  private
    module S = Group Self

  open Homomorphism S.Data S.Data S._==_

  record IsGroupAutomorphism (π•„βŸ¦_⟧ : Morphism) : Set (f βŠ” β„“) where
    field
      is-homomorphism : IsGroupHomomorphism Self Self π•„βŸ¦_⟧

Toward Isomorphism

An group isomorphism is a homomorphism with an additional property - bijection (one-to-one + onto). Bijection implies an isomorphism is a homomorphism such that the inverse of the homomorphism is also a homomorphism. Practically, an isomorphism is an equivalence relation. Often in mathematics one encounters the phrase β€œequal upto isomorphism” meaning isomorphism serves as equality for all practical purposes.

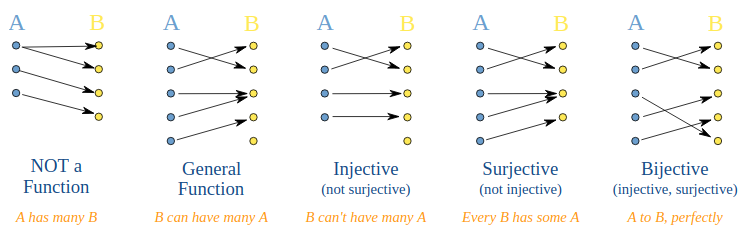
Injection vs Surjection vs Bijection

An injective morphism is a Monomorphism. A surjective morphism is an Epimorphism. An isomorphism is both injective and surjective.

Monomorphisms

We first define Monomorphisms:

Magma Monomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Magma f ℓ₁) (To : Magma t β„“β‚‚) where
  private
    module F = Magma From
    module T = Magma To

  open Homomorphism F.Data T.Data T._==_

  record IsMagmaMonomorphism (π•„βŸ¦_⟧ : Morphism) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-magma-homomorphism   : IsMagmaHomomorphism From To π•„βŸ¦_⟧
      is-morphism-injective   : Injective π•„βŸ¦_⟧

Semigroup Monomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Semigroup f ℓ₁) (To : Semigroup t β„“β‚‚) where
  private
    module F = Semigroup From
    module T = Semigroup To

  open Homomorphism F.Data T.Data T._==_

  record IsSemigroupMonomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-magma-monomorphism  : IsMagmaMonomorphism F.magma T.magma π•„βŸ¦_⟧

    open IsMagmaMonomorphism is-magma-monomorphism public

Monoid Monomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Monoid f ℓ₁) (To : Monoid t β„“β‚‚) where
  private
    module F = Monoid From
    module T = Monoid To

  open Homomorphism F.Data T.Data T._==_

  record IsMonoidMonomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-semigroup-monomorphism  : IsSemigroupMonomorphism F.semigroup T.semigroup π•„βŸ¦_⟧
      preserves-identity         : identity-preservation π•„βŸ¦_⟧ F.Ξ΅ T.Ξ΅

    open IsSemigroupMonomorphism is-semigroup-monomorphism public

Group Monomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Group f ℓ₁) (To : Group t β„“β‚‚) where
  private
    module F = Group From
    module T = Group To

  open Homomorphism F.Data T.Data T._==_

  record IsGroupMonomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-monoid-monomorphism  : IsMonoidMonomorphism F.monoid T.monoid π•„βŸ¦_⟧
      preserves-inverse       : compose-unary π•„βŸ¦_⟧ F._⁻¹ T._⁻¹

    open IsMonoidMonomorphism is-monoid-monomorphism public

Isomorphism

Now adding the condition of Surjectivity, we get isomorphisms:

Magma isomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Magma f ℓ₁) (To : Magma t β„“β‚‚) where
  private
    module F = Magma From
    module T = Magma To

  open Homomorphism F.Data T.Data T._==_

  record IsMagmaIsomorphism (π•„βŸ¦_⟧ : Morphism) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-magma-monomorphism   : IsMagmaMonomorphism From To π•„βŸ¦_⟧
      is-morphism-surjective  : Surjective π•„βŸ¦_⟧

Semigroup isomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Semigroup f ℓ₁) (To : Semigroup t β„“β‚‚) where
  private
    module F = Semigroup From
    module T = Semigroup To

  open Homomorphism F.Data T.Data T._==_

  record IsSemigroupIsomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-magma-isomorphism  : IsMagmaIsomorphism F.magma T.magma π•„βŸ¦_⟧

    open IsMagmaIsomorphism is-magma-isomorphism public

Monoid Isomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Monoid f ℓ₁) (To : Monoid t β„“β‚‚) where
  private
    module F = Monoid From
    module T = Monoid To

  open Homomorphism F.Data T.Data T._==_

  record IsMonoidIsomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-semigroup-isomorphism  : IsSemigroupIsomorphism F.semigroup T.semigroup π•„βŸ¦_⟧
      preserves-identity         : identity-preservation π•„βŸ¦_⟧ F.Ξ΅ T.Ξ΅

    open IsSemigroupIsomorphism is-semigroup-isomorphism public

Group Isomorphism

module _ {f t ℓ₁ β„“β‚‚} (From : Group f ℓ₁) (To : Group t β„“β‚‚) where
  private
    module F = Group From
    module T = Group To

  open Homomorphism F.Data T.Data T._==_

  record IsGroupIsomorphism (π•„βŸ¦_⟧ : Morphism ) : Set (f βŠ” t βŠ” ℓ₁ βŠ” β„“β‚‚) where
    field
      is-monoid-isomorphism  : IsMonoidIsomorphism F.monoid T.monoid π•„βŸ¦_⟧
      preserves-inverse       : compose-unary π•„βŸ¦_⟧ F._⁻¹ T._⁻¹

    open IsMonoidIsomorphism is-monoid-isomorphism public

Rings and family