open import Types.relations
open import Types.equality renaming (refl to ≡-refl)
open import Types.functions
open import Types.product
open import Algebra.sets
open import Agda.Primitive using (Level; _⊔_; lsuc; lzero)
module Algebra.groups {a ℓ} {A : Set a} (_==_ : Rel A ℓ) where
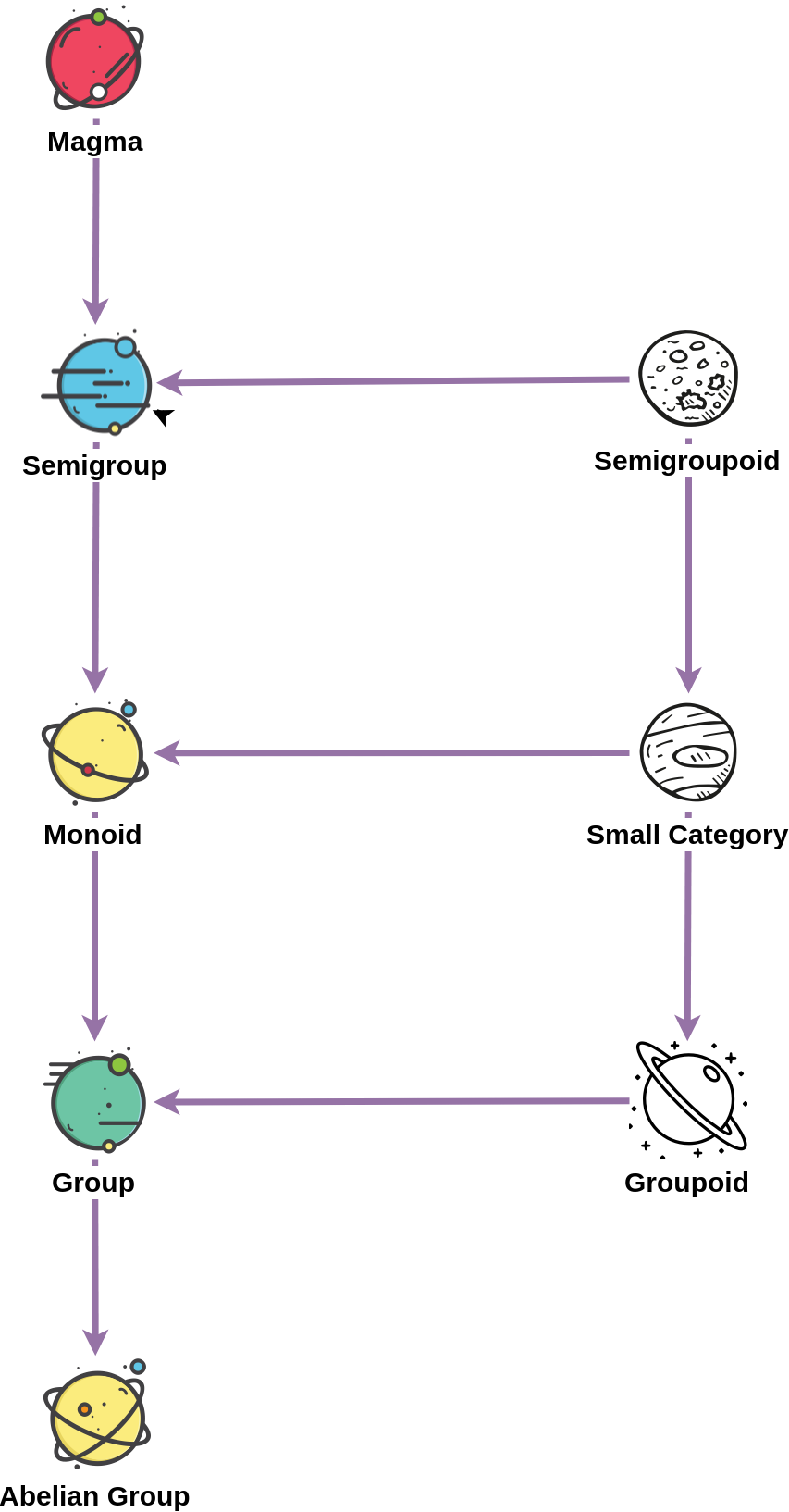
open import Types.operations (_==_)Group-like objects form another family of objects probed in abstract algebra. They have a similar pattern of building
like ordered objects but are more complex. This family contains of a set of type A and a binary operation
⋅ defined on that set which satisfy a bunch of properties. As there are a large number of properties to
choose from, one can end up with a large number of families, however here we describe only a few that generally
matter.
| Object ↓ Laws → | Totality | Associativity | Identity | Invertibility | Commutativity |
|---|---|---|---|---|---|
| Magma | ★ | ||||
| Semigroupoid | ★ | ||||
| Small Category | ★ | ★ | |||
| Quasigroup | ★ | ★ | |||
| Loop | ★ | ★ | ★ | ||
| Semigroup | ★ | ★ | |||
| Inverse Semigroup | ★ | ★ | ★ | ||
| Groupoid | ★ | ★ | ★ | ||
| Monoid | ★ | ★ | ★ | ||
| Group | ★ | ★ | ★ | ★ | |
| Abelian group | ★ | ★ | ★ | ★ | ★ |
Note that we implement only the packaged version of laws here, the actual object types we define in the next section Groups and family 2, this is because we cannot have two high level modules per agda file.

As we see above, semigroupoid is a generalization of the semigroup, group is a stricter form of a monoid or all groups are also monoids etc. Semigroupoids, Small Categories and Groupoids form what is called as partial abstract algebra such that they don’t require the totality property which thus allows their operations to be partial functions.
A magma is a set of objects with a closed binary operation defined on them. It is one of the simplest objects in abstract algebra.
A magma is a structure containing:
∙where:
∙ is closed, i.e. ∀ x y ∈ 𝔽, (x ∙ y) ∈ 𝔽 or ∙ : 𝔽 × 𝔽 → 𝔽 record IsMagma (∙ : ★ A) : Set (a ⊔ ℓ) where
field
∙-cong : Congruent₂ ∙
isEquivalence : IsEquivalence _==_
open IsEquivalence isEquivalence public
setoid : Setoid a ℓ
setoid = record { isEquivalence = isEquivalence }
-- satisfies congruence with underlying equivalence
∙-congˡ : LeftCongruent ∙
∙-congˡ y==z = ∙-cong y==z rfl
∙-congʳ : RightCongruent ∙
∙-congʳ y==z = ∙-cong rfl y==zMagmas are a nice start but are yet too general to be useful. Lets add more structure.
A semigroup is a structure where the operation is associative.
A semigroup is a structure containing:
∙where:
∙ is closed, i.e. ∀ x y ∈ 𝔽, (x ∙ y) ∈ 𝔽 or ∙ : 𝔽 × 𝔽 → 𝔽∙ is associative, i.e. x ∙ (y ∙ z) == (x ∙ y) ∙ z record IsSemigroup (∙ : ★ A) : Set (a ⊔ ℓ) where
field
isMagma : IsMagma ∙
assoc : Associative ∙
open IsMagma isMagma publicSemigroups are any data structure which support an addition operation but does not have a unit element.
A monoid is a semigroup, with a special element called the identity element. Monoids and semigroups are perhaps of
most significance to programmers as these are widely used to model various types and operations on them. For example,
JSON objects and a merge operation on them form a monoid. Strings and string concatenation form monoids
too.
Here are a few examples of monoids:
| Object | Operation | Identity |
|---|---|---|
| int | addition | 0 |
| int | subtraction | 0 |
| int | multiplication | 1 |
| float | addition | 0.0 |
| float | subtraction | 0.0 |
| float | multiplication | 1.0 |
| JSON | merge two JSONs | {} |
| JSON | create / delete / modify a key-value pair | {} |
| JSON | λ : JSON<A, B>, JSON<A, B> → JSON<A, B> |
{} |
| string | concatenation | '' |
| List / Array | concatenation | [] |
Monoidal operations (∙ : A × A → A) take two elements and “reduce” or “combine” them into one. In other
words they can be used to model types that can be aggregated arbitrarily, as one could take pairs of objects from a
monoid and combine them with the monoidal operation ∙ : A × A → A. This combination is independent of
whether it is done in synchronous, concuirrent or in parallel on a computer.
A monoid is a structure containing:
∙where:
∙ is closed, i.e. ∀ x y ∈ 𝔽, (x ∙ y) ∈ 𝔽 or ∙ : 𝔽 × 𝔽 → 𝔽∙ is associative, i.e. x ∙ (y ∙ z) == (x ∙ y) ∙ z∙ has an identity, i.e. ∃ i ∈ A, i ∙ i = i record IsMonoid (∙ : ★ A) (x : A) : Set (a ⊔ ℓ) where
field
isSemigroup : IsSemigroup ∙
identity : Identity x ∙
open IsSemigroup isSemigroup public
-- utils
identityˡ : LeftIdentity x ∙
identityˡ = fst identity
identityʳ : RightIdentity x ∙
identityʳ = snd identityA commutative monoid is a monoid with its operation required to be commutative.
A commutative monoid is a structure containing:
∙where:
∙ is closed, i.e. ∀ x y ∈ 𝔽, (x ∙ y) ∈ 𝔽 or ∙ : 𝔽 × 𝔽 → 𝔽∙ is associative, i.e. x ∙ (y ∙ z) == (x ∙ y) ∙ z∙ has an identity, i.e. ∃ i ∈ A, i ∙ i = i∙ is commutative, i.e. x ∙ y = y ∙ x record IsCommutativeMonoid (∙ : ★ A) (x : A) : Set (a ⊔ ℓ) where
field
isMonoid : IsMonoid ∙ x
comm : Commutative ∙
open IsMonoid isMonoid publicA group is a monoid with the additional requirement of the binary operation to have an inverse operation for every pair of elements of the group. A group is another widely-used structure.
| Field | Used to model |
|---|---|
| Physics | Symmetry in Noether’s theorem |
| Physics | Gauge theories (quantum electrodynamics, quantum field theory) |
| Physics | Gauge formulation of general relativity |
| Physics | M-brane theory (and other string theories) |
| Chemistry | Classification of crystal structure |
| Chemistry | Symmetries of molecules |
| Cryptography | ECDSA (Elliptic Curve Digital Signature Algorithm) signatures |
A group is a structure containing:
∙where:
∙ is closed, i.e. ∀ x y ∈ 𝔽, (x ∙ y) ∈ 𝔽 or ∙ : 𝔽 × 𝔽 → 𝔽∙ is associative, i.e. x ∙ (y ∙ z) == (x ∙ y) ∙ z∙ has an identity, i.e. ∃ i ∈ A, i ∙ i = ix has an inverse x⁻¹, such that ((x ⁻¹) ∙ x) == i record IsGroup (_∙_ : ★ A) (x : A) (_⁻¹ : ♠ A) : Set (a ⊔ ℓ) where
field
isMonoid : IsMonoid _∙_ x
inverse : Inverse x _⁻¹ _∙_
⁻¹-cong : Congruent₁ _⁻¹
open IsMonoid isMonoid public
infixl 7 _-_
_-_ : ★ A
x - y = x ∙ (y ⁻¹)
inverseˡ : LeftInverse x _⁻¹ _∙_
inverseˡ = fst inverse
inverseʳ : RightInverse x _⁻¹ _∙_
inverseʳ = snd inverse
open import Types.equational2
open withCongruence _==_ _∙_ _⁻¹ rfl trans sym ∙-cong x public
-- uniqueness of the inverses
uniqueˡ-⁻¹ : ∀ α β → (α ∙ β) == x → α == (β ⁻¹)
uniqueˡ-⁻¹ = assoc+id+invʳ⇒invˡ-unique assoc identity inverseʳ
uniqueʳ-⁻¹ : ∀ α β → (α ∙ β) == x → β == (α ⁻¹)
uniqueʳ-⁻¹ = assoc+id+invˡ⇒invʳ-unique assoc identity inverseˡAn Abelian group, named after Niels Henrik Abel, is a group and requires its operation to also be commutative.
An abelian group is a structure containing:
∙where:
∙ is closed, i.e. ∀ x y ∈ 𝔽, (x ∙ y) ∈ 𝔽 or ∙ : 𝔽 × 𝔽 → 𝔽∙ is associative, i.e. x ∙ (y ∙ z) == (x ∙ y) ∙ z∙ has an identity, i.e. ∃ i ∈ A, i ∙ i = i∙ is commutative, i.e. x ∙ y = y ∙ xx has an inverse x⁻¹, such that ((x ⁻¹) ∙ x) == i record IsAbelianGroup (∙ : ★ A) (x : A) (⁻¹ : ♠ A) : Set (a ⊔ ℓ) where
field
isGroup : IsGroup ∙ x ⁻¹
comm : Commutative ∙
open IsGroup isGroup public
isCommutativeMonoid : IsCommutativeMonoid ∙ x
isCommutativeMonoid = record
{ isMonoid = isMonoid
; comm = comm
}