open import Agda.Primitive using (Level; _⊔_; lsuc; lzero)
open import Types.relations
open import Types.equality
open import Types.product using (Σ; _,_; _∪_)
module Algebra.order {a ℓ} {A : Set a} (_==_ : Rel A ℓ) whereThe equivalence relation remains the most basic relation to be built on objects of all kinds. Higher relations which tend to impose further structural constraints on objects thus creating richer objects and their APIs capable of modeling more complex phenomenon (not much unlike how a programming language’s expressiveness enables one to build more complex programs).
Order is one such higher relation and is fundamental in building a class of structures. There are different kinds of ordered relations each with progressively stricter laws.
| Relation | Reflexivity | Transitivity | Antisymmetry | Total |
|---|---|---|---|---|
| Pre-order | ★ | ★ | ||
| Partial-order | ★ | ★ | ★ | |
| Total order | ★ | ★ | ★ | ★ |
Preorders are binary relations (~ : A → A) on a type A where:
~ is reflexive, i.e. x ∼ x~ is transitive, i.e. x ∼ y and y ∼ z ⇒ x ∼ zPreorders are relations which are reflexive and transitive.
We first define an object that encapsulates all the rules into one record:
record IsPreorder (_∼_ : Rel A ℓ) : Set (a ⊔ ℓ) where
field
reflexive : Reflexive _∼_
trans : Transitive _∼_These are rather quite abstract to be actually useful and we need more structure to get things interesting.
Partial orders are a subtype of pre-orders where ≤ : A → A:
≤ is reflexive, i.e. x ≤ x≤ is transitive, i.e. x ≤ y and y ≤ z ⇒ x ≤ z≤ is antisymmetric, i.e. x ≤ y and y ≤ x ⇒ x = yA partial order, or partially ordered set or Poset, is an antisymmetric preorder. In plain words, we require the
relation _≤_ to have the property of antisymmety with respect to the underlying equality. Antisymmetry
makes posets very useful as they have unique maximum (called “supremum” or least upper bound) and minimum (called
“infimum” or greatest lower bound). This property makes posets satisfy the properties of being a lattice which support a
boolean algebra-like mechanics, which we shall see later. Posets also play an important role in algebraic geometry.
A relation _≤_ is anti-symmetric over the underlying equality _==_, if for every
x, y,
\[ x ≤ y , y ≤ x ⟹ x == y \]
Antisymmetric : Rel A ℓ → Rel A ℓ → Set _
Antisymmetric _==_ _≤_ = ∀ {x y} → x ≤ y → y ≤ x → x == yWe can now define partially ordered sets:
record IsPartialOrder (_≤_ : Rel A ℓ) : Set (a ⊔ ℓ) where
field
isPreorder : IsPreorder _≤_
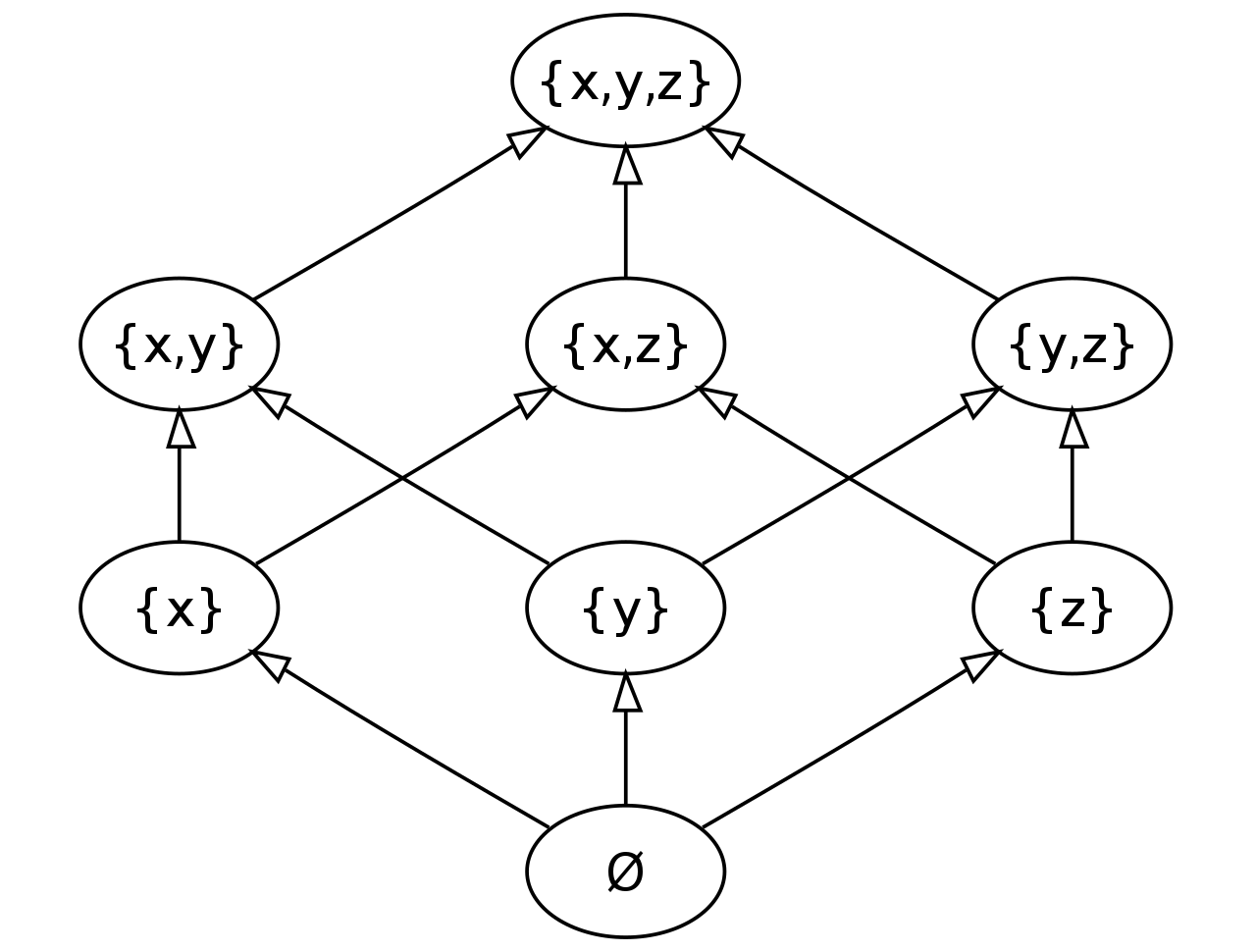
antisym : Antisymmetric _==_ _≤_A “Power set” of a set of objects S is the set of all subsets of S, including the empty set and S
itself, denoted by ℙ(S). Every power set is a poset.

The following are more examples: The real numbers ordered by the standard less-than-or-equal relation ≤.
The set of natural numbers equipped with the relation of divisibility. The vertex set of a directed acyclic graph
ordered by reachability.
Total orders are binary relations ≤ : A → A where:
≤ is reflexive, i.e. x ≤ x≤ is transitive, i.e. x ≤ y and y ≤ z ⇒ x ≤ z≤ is antisymmetric, i.e. x ≤ y and y ≤ x ⇒ x = y≤ is a total relation, i.e. ∀ x and y : x ≤ y or y ≤ xTotal orders are a further constrained subtype of posets. All pairs of elements contained in a poset need not be
comparable. This is exactly what total orders represent. A total order is a total preorder, or the preorder’s relation
_≤_ to be a total function.
A relation _≤_ is total if x ≤ y or y ≤ x. This relation has to exist between
any pair of elements of A:
Total : {A : Set a} → Rel A ℓ → Set _
Total _∼_ = ∀ x y → (x ∼ y) ∪ (y ∼ x)We can now define total orders:
record IsTotalOrder (_≤_ : Rel A ℓ) : Set (a ⊔ ℓ) where
field
isPartialOrder : IsPartialOrder _≤_
total : Total _≤_
open IsPartialOrder isPartialOrder public