Contents Previous Next

Category

open import Agda.Primitive using (Level; _βŠ”_; lsuc; lzero)

open import Types.product
open import Types.relations
open import Types.equality

module Category.category where

A category is the object of study in category theory. It can be thought of being a bunch of objects, which are associated by a bunch of arrows between those objects, with the arrows being composable and each object having unit arrows. This minimal structure ensures a multitude of object types studied in mathematics can fit the description.

A category β„‚ consists of:

  1. A collection of objects \(x \in obj(β„‚)\)
  2. A collection of morphisms between those objects \(hom(𝕔) = \{ f : a β†’ b : a,b ∈ β„‚ \}\), called a β€œhom” set

such that:

  1. Morphisms compose:

If \[f : a β†’ b, g : b β†’ c\] then \[g ∘ f : a β†’ c\]

  1. Morphisms are associative:

\[If~~ f : a β†’ b,~ g : b β†’ c ~~and~~ h : c β†’ d ~~then~~ h ∘ (g ∘ f) = (h ∘ g) ∘ f\]

Figure 1: Composition
  1. Morphisms have identities: For every object x, there exists a morphism \(1β‚“ : x β†’ x\) called the identity morphism for x, such that for every morphism \(f : a β†’ x\) and every morphism \(g : x β†’ b\), we have \(1β‚“ ∘ f = f\) and \(g ∘ 1β‚“ = g\).
record Category (o β„“ e : Level) : Set (suc (o βŠ” β„“ βŠ” e)) where
  infix  4 _β‰ˆ_ _β‡’_
  infixr 9 _∘_

  field
    Obj : Set o                     -- objects
    _β‡’_ : Rel Obj β„“                 -- morphism
    _β‰ˆ_ : βˆ€ {A B} β†’ Rel (A β‡’ B) e   -- equivalence of morphisms
    id  : βˆ€ {A} β†’ (A β‡’ A)           -- identity

    -- composition of morphisms
    _∘_ : βˆ€ {A B C} β†’ (B β‡’ C) β†’ (A β‡’ B) β†’ (A β‡’ C)

    -- laws
    -- satisfy associativity
    assoc     : βˆ€ {A B C D} {f : A β‡’ B} {g : B β‡’ C} {h : C β‡’ D} β†’ (h ∘ g) ∘ f β‰ˆ h ∘ (g ∘ f)
    -- satisfy identity
    identityΛ‘ : βˆ€ {A B} {f : A β‡’ B} β†’ id ∘ f β‰ˆ f
    identityΚ³ : βˆ€ {A B} {f : A β‡’ B} β†’ f ∘ id β‰ˆ f
    -- has an equivalence for morphisms
    equiv     : βˆ€ {A B} β†’ IsEquivalence (_β‰ˆ_ {A} {B})
    -- composition is congruent on equivalence
    ∘-resp-β‰ˆ  : βˆ€ {A B C} {f h : B β‡’ C} {g i : A β‡’ B} β†’ f β‰ˆ h β†’ g β‰ˆ i β†’ f ∘ g β‰ˆ h ∘ i

Opposite Category

The machinery of category theory also admits a duality, like an object and its mirror image. The opposite or dual of a category \(β„‚\), denoted by \(β„‚α΄Όα΅–\), is the same category, but with all morphisms in the opposite direction. All laws and machinery of category theory have their dual versions.

record Categoryα΄Όα΅– (o β„“ e : Level) : Set (suc (o βŠ” β„“ βŠ” e)) where
  infix  4 _β‰ˆ_ _β‡’_
  infixr 9 _∘_

  field
    Obj : Set o                     -- objects
    _β‡’_ : Rel Obj β„“                 -- morphism
    _β‰ˆ_ : βˆ€ {A B} β†’ Rel (B β‡’ A) e   -- equivalence of morphisms
    id  : βˆ€ {A} β†’ (A β‡’ A)           -- identity

    -- composition of morphisms
    _∘_ : βˆ€ {A B C} β†’ (B β‡’ A) β†’ (C β‡’ B) β†’ (C β‡’ A)

    -- laws
    -- satisfy associativity
    assoc     : βˆ€ {A B C D} {f : A β‡’ B} {g : B β‡’ C} {h : C β‡’ D} β†’ h ∘ (g ∘ f) β‰ˆ (h ∘ g) ∘ f
    -- satisfy identity
    identityΛ‘ : βˆ€ {A B} {f : A β‡’ B} β†’ id ∘ f β‰ˆ f
    identityΚ³ : βˆ€ {A B} {f : A β‡’ B} β†’ f ∘ id β‰ˆ f
    -- has an equivalence for morphisms
    equiv     : βˆ€ {A B} β†’ IsEquivalence (_β‰ˆ_ {A} {B})
    -- composition is congruent on equivalence
    ∘-resp-β‰ˆ  : βˆ€ {A B C} {f h : B β‡’ C} {g i : A β‡’ B} β†’ g β‰ˆ i β†’ f β‰ˆ h β†’ g ∘ f β‰ˆ i ∘ h

Examples

We can use various mathematical structures to construct categories out of. When defining a category, we have to decide what our objects and our morphisms would be and how would the morphisms compose. This decision has to be taken in a way that the conditions of being a category are satisfied (associativity, identity). We would then have a category of our chosen object.

Category of Sets

A category of sets is the simplest of categories we can construct and the most intuitive to understand given we have been trained to think in terms of sets.

Category of Groups

Category of Rings

Category of Topological Spaces

Here are some other examples:

Category Objects Morphisms
Set sets total functions
Group groups group homomorphisms
Top topological spaces continuous functions
Vectβ‚– vector spaces over field K linear transformations
Poset partially ordered sets order-preserving functions
TopVect topological vector spaces continuous linear maps
𝕄 differentiable manifolds differentiable maps
Banach spaces open subsets of Banach spaces differentiable maps
𝕍 vector bundles vector bundle maps

There are in fact infinitely many more and so we are going to move along now.

Nerves of Categories

Simplicial Complexes

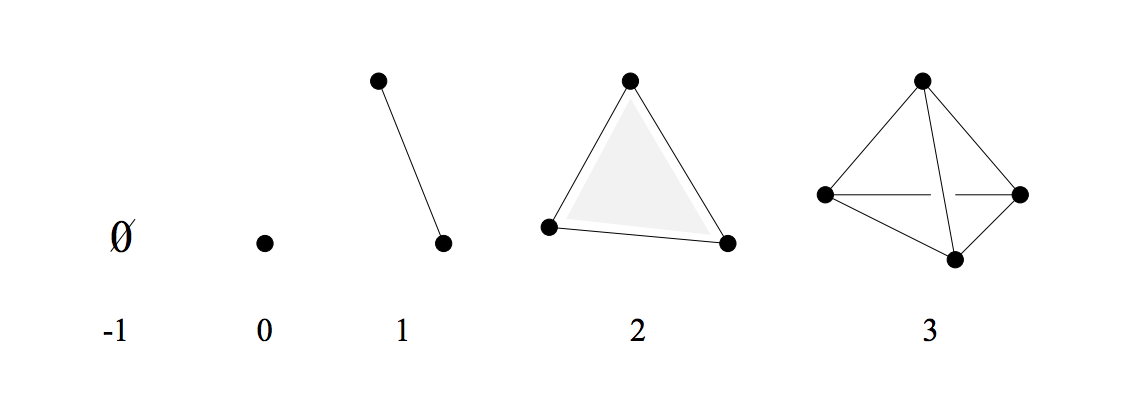
Before explaining higher categories, let us look at a structure from algebraic topology called simplexes and simplicial complexes.

Simplexes

A simplex is an n-dimensional β€œtriangle”. Some examples of the first few dimensional simplices are:

An n-dimensional simplex is also called an (n+1)-cell.

Figure 5: Simplices

Simplicial Complexes

A simplicial complex is a structure formed by gluing together a bunch of simplices. The gluing process has to follow a set of properties:

A set of simplices \(\mathcal{K}\) is a simplicial complex if: - Every face of a simplex from \(\mathcal{K}\) is also in \(\mathcal{K}\) - Intersections of any two simplices is a face of both the simplices

A simplicial complex is of dimension n if the largest dimension of all the constituent simplices is n.

\[ dim(\mathcal{K}) = max(dim(Οƒ_i)) \]

Examples:

Simplicial complexes can be used to create or represent topological spaces and serve as a very useful tool. They can also be used to formalize algebraic constraints in geometric terms as well.

The Nerve N(β„‚) of a category β„‚ is a simplicial complex constructed from objects as vertices of simplices and morphisms of β„‚ as the edges.

Figure 2: Nerves of a category

Constructions of Categories

Product Category

Given two (or more) categories, their cartesian product is also a category.

Given two categories β„‚ and 𝔻, their product is a category with: - Pairs (C, D) as objects such that C ∈ β„‚ and D ∈ 𝔻 - (f, g) as morphisms where - \(f : C_1 β†’ C_2; C_i ∈ β„‚\) - \(g : D_1 β†’ D_2; D_i ∈ 𝔻\) - composition of morphisms defined as \((f_1, g_1) ∘ (f_2, g_2) = (f_1 ∘ f_2, g_1 ∘ g_2)\) - identities defined as \(1_{(C, D)} = (1_C, 1_D)\)

Free Category

Free categories are a result of using a general pattern called β€œfree constructions” for building categories. The idea of free objects in mathematics can be related to all types of objects with algebraic structure, and provides a general method of constructing objects using a set of β€œconstructor” objects. The process of construction proceeds as follows:

  1. Take a set of objects to construct the free category with
  2. Construct all possible combinations of these objects, in other words, the power set of the set of those objects. These form the algebraic object of interest
  3. Define relations between every pair of objects according to the kind of algebraic object to construct

For free categories these rules become:

  1. Consider a bunch of objects to be taken as generators
  2. Construct the power set of these generators, these form the objects of the free category
  3. Define morphisms between every pair of objects and all compositions of their morphisms, together they form the hom-set of the free category

Morphisms