open import Agda.Primitive using (Level; _⊔_; lsuc; lzero)
open import Types.product
open import Types.relations
open import Types.equality
open import Category.category
module Category.morphisms whereMorphisms are structure-preserving maps from one mathematical structure to another of the same type. They are a generalized notion that translates to group homomorphisms for groups, ring homomorphisms for rings, continuous maps for vector spaces and so on. In the context of category theory, these morphisms have to admit the properties of composition and associativity.
A morphism \(f : X → Y\) is called a Monomorphism if \(f ∘ g_1 = f ∘ g_2\) implies \(g_1 = g_2\) for all \(g_1, g_2 : A → X\). A monomorphism is called “mono” in short and “monic” can be used as an adjective to describe such a morphism.

Epimorphisms are dual objects to monomorphisms. A morphism \(f : X → Y\) is called an Epimorphism if \(g_1 ∘ f = g_2 ∘ f\) implies \(g_1 = g_2\) for all \(g_1, g_2 : Y → A\). An Epimorphism is called “epi” in short and “epic” can be used as an adjective to describe such a morphism.
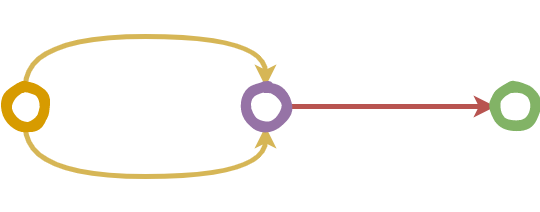
A morphism \(f: X → Y\) has a left inverse if there is a morphism \(g: Y → X\) such that \(g ∘ f = id_X\). The left inverse g is also called a retraction of f. Morphisms with left inverses are always monomorphisms, but the converse is not true in general; a monomorphism may fail to have a left inverse. If a retraction exists for a function f, it can also be expected to be injective.
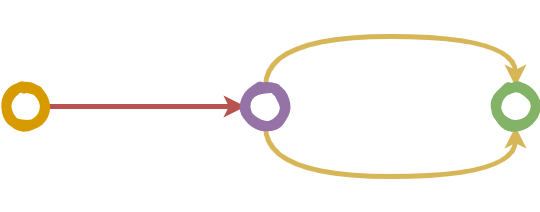
A morphism \(f: X → Y\) has a right inverse if there is a morphism \(g: Y → X\) such that \(f ∘ g = id_Y\). The right inverse g is also called a section of f. Morphisms having a right inverse are always epimorphisms, but the converse is not true in general, as an epimorphism may fail to have a right inverse. If a section exists for a function f, it can also be expected to be surjective.
Endomorphisms are morphisms with the same source and target, \(f : X → X\).
A morphism \(f : X → Y\) is called an isomorphism if there exists a unique morphism \(g: Y → X\) such that \(f ∘ g = id_Y\) and \(g ∘ f = id_X\). If a morphism has both left-inverse and right-inverse, then the two inverses are equal, so f is an isomorphism, and g is called simply the inverse of f.
An automorphism is both an endomorphism and an isomorphism.