Contents Previous Next

• Functors
• Covariance and Contravariance
• Opposite Functors
• Hom Functors
  • Covariant Hom-Functor
  • Contravariant Hom-Functor
• Bifunctors and multifunctors
• Endofunctor
• Forgetful Functor
• Free Functor
• Representable Functor

Functors

open import Agda.Primitive using (Level; _⊔_; lsuc; lzero)

open import Types.product
open import Types.relations
open import Types.equality
open import Category.category
open import Category.morphisms

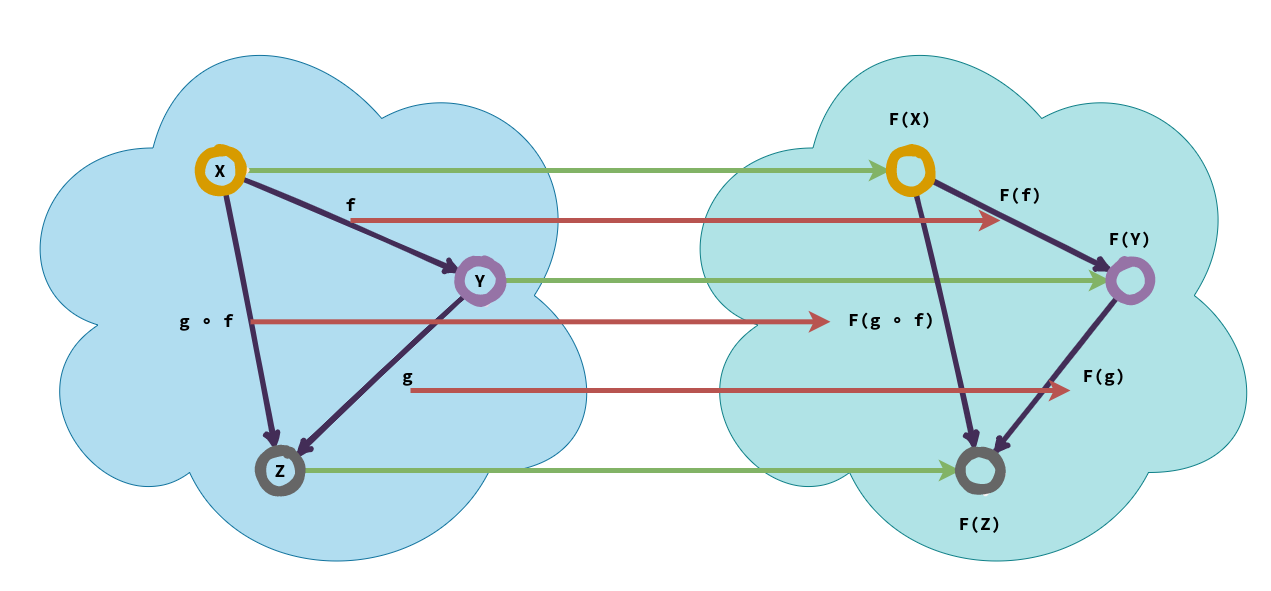
module Category.functors where

Functors can be thought of as structure preserving maps or functions that operate on one category to produce another category, maintaining the categorical structure of the first category in the second category. Functors operate on both objects and morphisms of the first category.

Formally, let ℂ and 𝔻 be two categories, then a functor 𝔽 between them:

• Takes every object c ∈ ℂ to an object 𝔽(c) ∈ 𝔻
• Takes every morphism \(f : c_1 → c_2\) ∈ ℂ to a morphism \(𝔽(f) : 𝔽(c_1) → 𝔽(c_2)\) in 𝔻 such that:
  • \(𝔽(id_c) = id_{𝔽(c)}\)
  • \(𝔽(g ∘ f) = 𝔽(g) ∘ 𝔽(f)\) for all \(f : c_1 → c_2\) and \(g : c_2 → c_3\) ∈ ℂ

Thus, functors preserve composition and identity morphisms of the source category in the target category.

Covariance and Contravariance

Covariant functors are the vanilla functors we discussed in the previous section.

Contravariant functors are similar to covariant functors except that the functor reverses the direction of arrows in the target category.

Formally, let ℂ and 𝔻 be two categories, then a contravariant functor 𝔽 between them:

• Takes every object c ∈ ℂ to an object 𝔽(c) ∈ 𝔻
• Takes every morphism \(f : c_1 → c_2\) ∈ ℂ to a morphism \(𝔽(f) : 𝔽(c_2) → 𝔽(c_1)\) in 𝔻 such that:
  • \(𝔽(id_c) = id_{𝔽(c)}\)
  • \(𝔽(g ∘ f) = 𝔽(f) ∘ 𝔽(g)\) for all \(f : c_1 → c_2\) and \(g : c_2 → c_3\) ∈ ℂ

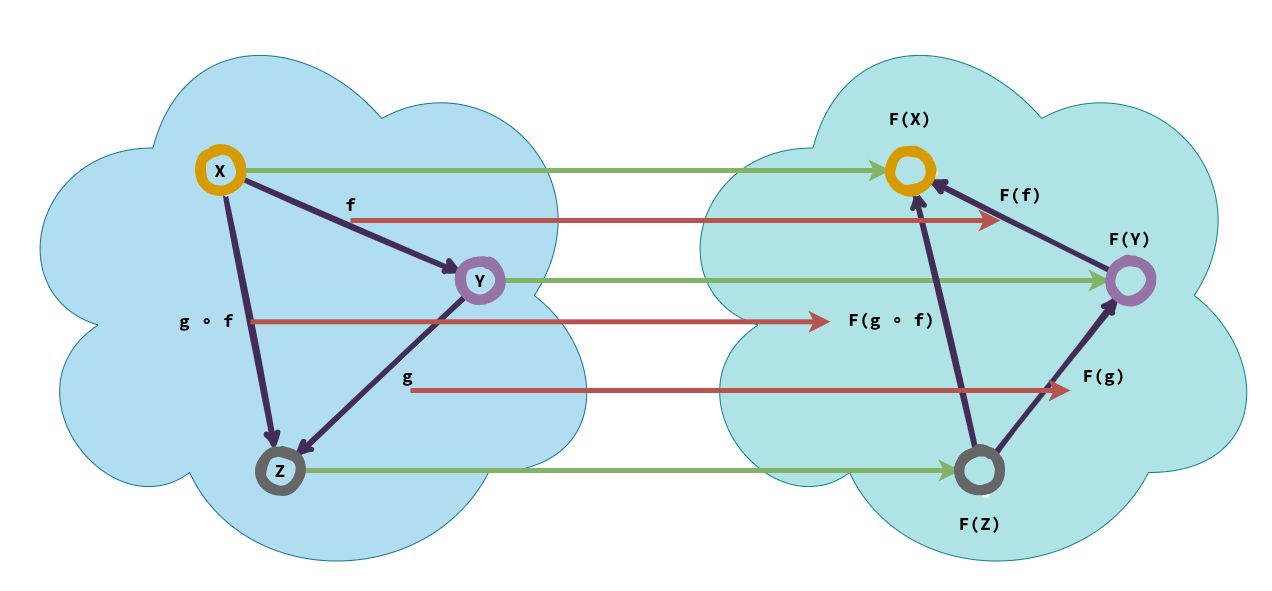
Contravariant functors thus produce opposite categories. They can also be thought of as covariant functors from \(ℂ^{op} → 𝔻\) or as \(ℂ → 𝔻^{op}\) depending upon which one is convenient for working with. Contravariant functors play a very important role in various fields of mathematics, the most mentionable ones being presheaves and sheaves in algebraic topology are contravariant functors with some extra structure.

Opposite Functors

Every functor \(𝔽 : ℂ → 𝔻\) induces the opposite functor \(𝔽^{op} : ℂ^{op} → 𝔻^{op}\) such that \((𝔽^{op})^{op} = 𝔽\).

Hom Functors

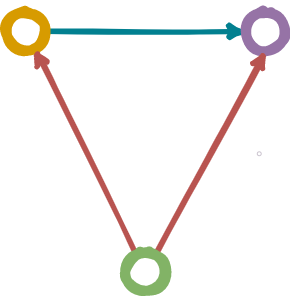
For a category ℂ, the set of all morphisms in ℂ is called the Hom-set. If we take any object A ∈ ℂ, then the functor that maps any object X ∈ ℂ to the set of morphisms from A to X, i.e. Hom(A, X), is called the covariant Hom-functor. Similarly, the functor that maps any object X in ℂ to the set of morphisms from X to A, i.e. Hom(X, A), is called a contravariant Hom-functor.

Covariant Hom-Functor

For a category ℂ and a fixed object A ∈ ℂ, a covariant Hom-functor \(Hom(A, −) : A → Set\):

• Maps each object X ∈ ℂ to the set of morphisms of ℂ, Hom(A, X)
• Maps each morphism \(f : X → Y\) to the morphism \(Hom(A, f) : Hom(A, X) → Hom(A, Y)\) where each h ∈ Hom(A, f) takes some g ∈ Hom(A, X) to \(f ∘ g\)

Contravariant Hom-Functor

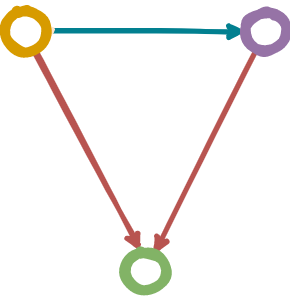
For a category ℂ and a fixed object A ∈ ℂ, a contravariant Hom-functor \(Hom(−, B) : B → Set\):

• Maps each object X ∈ ℂ to the set of morphisms of ℂ, Hom(X, B)
• Maps each morphism \(f : X → Y\) to the morphism \(Hom(f, B) : Hom(X, B) → Hom(Y, B)\) where each h ∈ Hom(f, A) takes some g ∈ Hom(Y, B) to \(g ∘ f\)

Bifunctors and multifunctors

We define categories of the form 𝔸×𝔹 which is a cartesian product of two categories 𝔸 and 𝔹 as Cartesian categories. Given two functors \(𝔽 : 𝔸 → 𝕏\) and \(𝔾 : 𝔹 → 𝕐\), we can define a functor on a product category 𝔸×𝔹 as the cartesian product of the individual functors 𝔽×𝔾. Such a functor is called a bifunctor. We can extend this notion to multifunctors.

Endofunctor

Endofunctors are functors that have the same source and target categories: \(𝔽 : ℂ → ℂ\).

Forgetful Functor

Functors where the source category has more structure that the functor “forgets” while mapping it to the target category with lesser structure is called a forgetful functor. A functor from the category of Groups to the category of Sets which maps a group to its underlying set and a group homomorphism to its underlying function of sets is an example of a forgetful functor.

Free Functor

A free functor is the dual of the forgetful functor − instead of forgetting structure, it adds structure to its source category to get the target category. This addition of structure is done by using the source category as generators for generating free target categories. The free functor from Sets to Groups sends every set X to the free group generated by X and functions between sets to homomorphisms between free groups.

Representable Functor

A representable functor sends a category to the category of sets. Representable functors represent an arbitrary category in the language of sets for studying the category in the more familiar language of sets.

Formally, a functor \(𝔽 : ℂ → Set\) is a representable functor if it is naturally isomorphic to the hom-functor \(Hom_{ℂ}(A, −)\), A ∈ ℂ.

• Sends every object \(X ∈ ℂ\) to the hom-set \(Hom_{ℂ}(X, A)\)
• sends morphisms \(f : X' → X\) to \(F : (X → A) → (X' → X → A)\)

Dually, a contravariant functor \(𝔾 : ℂ^{op} → Set\) is representable if it is naturally isomorphic to the contravariant hom-functor \(Hom_{ℂ}(−, A), A ∈ ℂ\).

• Sends every object \(X ∈ ℂ\) to the hom-set \(Hom_{ℂ^{op}}(A, X)\)
• sends morphisms \(f : X → X'\) to \(F : (X → A) → (X' → X → A)\)

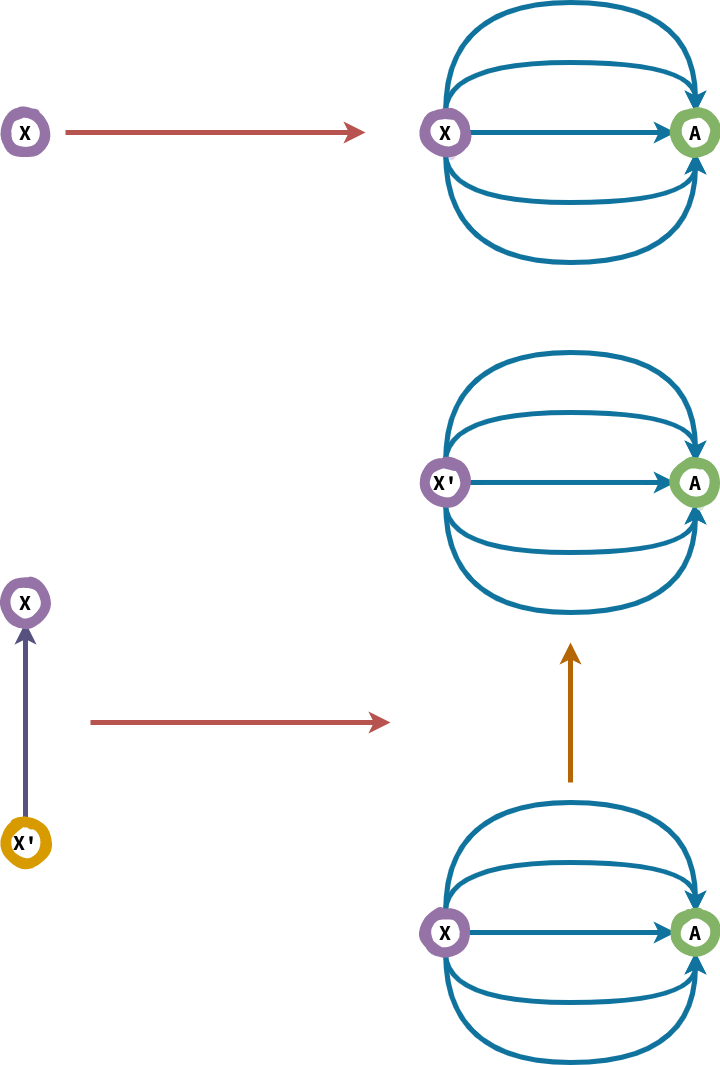
Though we have given a choppy definition of representable functors here without defining what “natural isomorphism” is, we will look deeper as they are one of the central concepts for building further structures of category theory.

Natural Transformations