Contents Previous Next

Natural Transformations

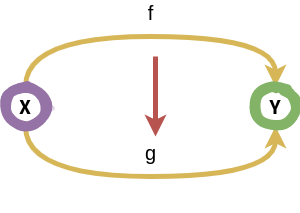
module Category.naturalTransformation where

Commutative Diagrams

Commutative diagrams are a great tool widely used in category to pictorially depict constraints rather than using mathematical equations. These diagrams are directed graphs with each node representing mathematical objects and the arrows between them represent morphisms.

A commutative diagram often consists of three parts:

A diagram is said to be commutative (or to commute) when if any two paths that connect the same two objects (no matter how many hops each path may have) arrive at the same result - it does not matter which path one takes to arrive at the end.

##️ Natural Transformations

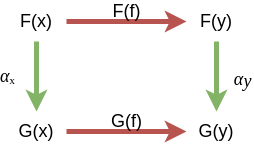
Natural transformations are structure preserving maps between functors. Just as a functor is a morphism between categories, a natural transformation is a morphism between two functors. Since it is at a higher level than functors, it can also be called a 2-morphism.

Figure 1: Natural Transformation

Given categories β„‚ and 𝔻 and functors \(F, G : β„‚ β†’ 𝔻\) and for some \(f : x β†’ y\), a natural transformation \(Ξ± : F β†’ G\) ensures the following diagram is satisfied (the following diagram β€œcommutes”):

Figure 2: Natural Transformation Commutative Diagram

Composition

Natural transformations can either be composed horizontally or vertically:

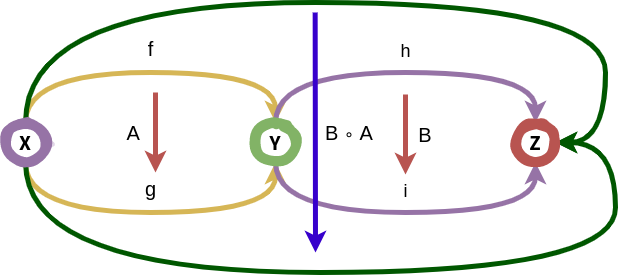
Figure 3: Horizontal Composition
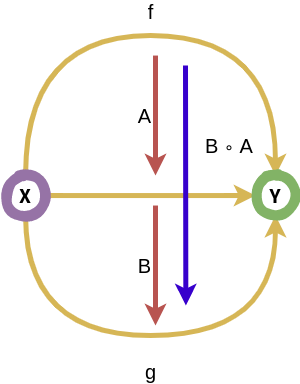
Figure 4: Vertical Composition

Both kinds of composition allows for the associativity law and identity natural transformations.

Functor Categories

As we have seen above, composition of natural transformations follows all the laws that morphisms follow in a category. We can take advantage of that fact and define a category of functors:

Given two categories β„‚ and 𝔻, we can define a category of functors with: - Functors \(F_i : β„‚ β†’ 𝔻\) as objects - Natural transformations \(Ξ· : F_i β†’ F_j\) as morphisms

The natural transformations between β„‚ and 𝔻 which are isomorphisms are also called Natural Isomorphisms.

The above definition of functor categories take into account only vertical compositions. We can also define a more general kind of functor categories, also called a 2-category:

Given a bunch of categories \(𝕔_i\), we can define a 2-category with: - categories \(𝕔_i\) as objects - Functors between \(𝕔_i\) as morphisms: \(F_{ij} : 𝕔_i β†’ 𝕔_j\) - Natural transformations between functors as 2-morphisms: \(Ξ· : F_{ij} β†’ F'_{ij}\) and \(Ξ³ : F_{ij} β†’ G_{jk}\)

Yoneda Lemma