Yoneda Lemma

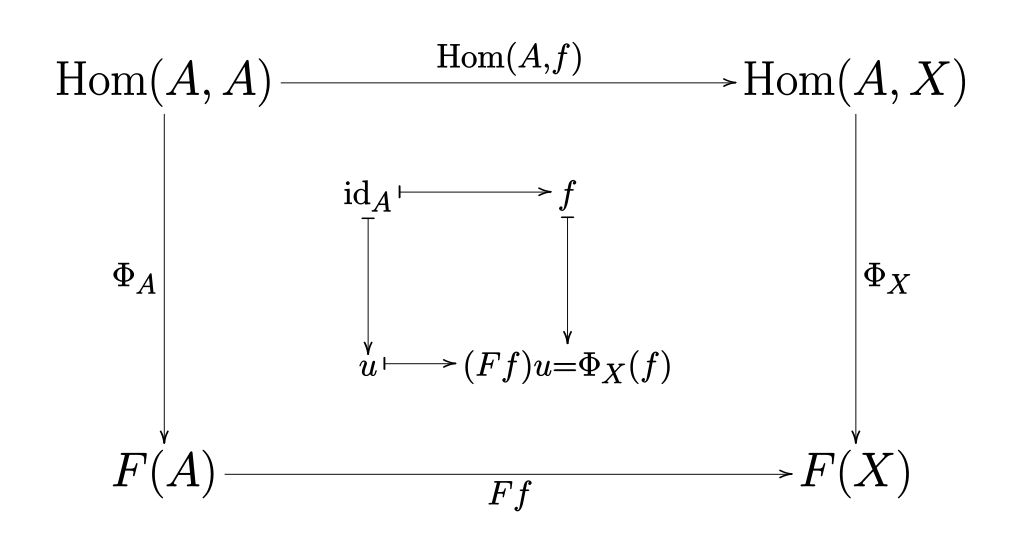
module Category.yonedaLemma where

The Yoneda lemma is considered one of the most important results in category theory. It basically states that an object can either be studied by itself (intrinsic) or in terms of all the relations that object has with the rest of the universe (extrinsic) and both ways are equivalent. In terms of category theory specifically, it implies that a category can be studied as a category or as the set of functors from that category into Set, the category of sets (representative functors).

For every object \(\mathcal{x}\) of a (locally small) category ℂ, there exists a functor to Set called the hom-functor \(h^{\mathcal{x}} = Hom(\mathcal{x}, −)\). For any arbitrary functor \(F : ℂ → Set\), the Yoneda lemma states:

\[ Nat(Hom(\mathcal{x}, −), F) ≅ F(\mathcal{x}) \]

is a natural isomorphism and is in one-to-one correspondence.

The right hand side \(F(\mathcal{x})\) is the functor from \(\mathcal{x}\) to Set, hence describes how \(\mathcal{x}\) interacts with F. This is the intrinsic view where an object is being directly studied.

However, the object \(\mathcal{x}\) is equal to all the functors from \(\mathcal{x}\) to Set, which is represented on the left hand side by the covariant hom-functor \(Hom(\mathcal{x}, −)\).

Now, if we consider the object \(F(\mathcal{x})\), we can apply similar treatment to it and get its hom-functor (which is also a natural transformation, hence Nat), which is \(Nat(Hom(\mathcal{x}, −), F)\).

Contravariant Version

Thanks to duality, there exists a contravariant version of the Yoneda lemma:

\[ Nat(Hom(−, \mathcal{x}), G) ≅ G(\mathcal{x}) \]

where \(Hom(−, \mathcal{x})\) is the contravariant hom-functor.

Yoneda Embedding

In the special case where the functor \(F\) is also a hom-functor from \(Hom(\mathcal{y}, −) : ℂ → Set\), the Yoneda lemma becomes:

\[ Nat(Hom(\mathcal{x}, −), Hom(\mathcal{y}, −)) ≅ Hom(\mathcal{y}, \mathcal{x}) \]

That is, natural transformations between hom-functors are in one-to-one correspondence with morphisms (in the reverse direction) between the associated objects. Thus one can use this to embed any category into the category of contravariant functors. This is called the Yoneda embedding.

Yoneda Lemma