module Types.functions2 where
open import Lang.dataStructures using (
Bool; true; false;
ℕ; List;
one; two; three; four; five; six; seven; eight; nine; ten; zero; succ;
_::_; [];
⊤; singleton; ⟂)
open import Agda.Primitive using (Level; _⊔_; lsuc)
open import Types.equality
open import Types.product using (Σ; _,_; fst; snd)
open import Types.functions
open import Types.equationalFunctions can be classified into:
Note that a function, by definition, can never produce multiple outputs given the same input.

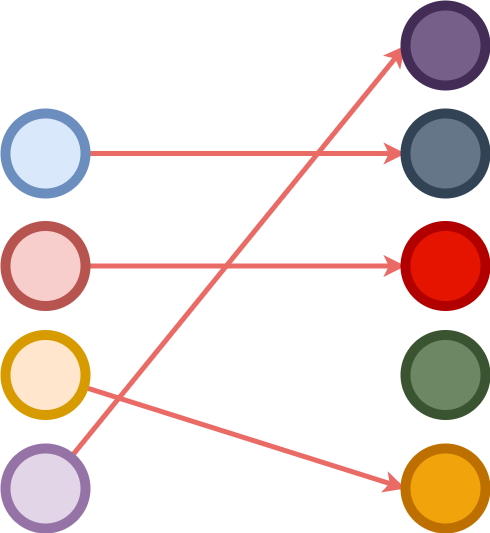
A function f : X → Y is injective if \(∀ x ∈ X, y ∈ Y, f(x) == f(y) ⟹ x ==
y\). Or in other words, the map is one-to-one between all objects of X and some objects of Y.
Injective : ∀ {a b} {A : Set a} {B : Set b} → (A → B) → Set (a ⊔ b)
Injective f = ∀ {x y} → f x ≡ f y → x ≡ y
record Injection {f t} (From : Set f) (To : Set t) : Set (f ⊔ t) where
field
to : From → To
injective : Injective to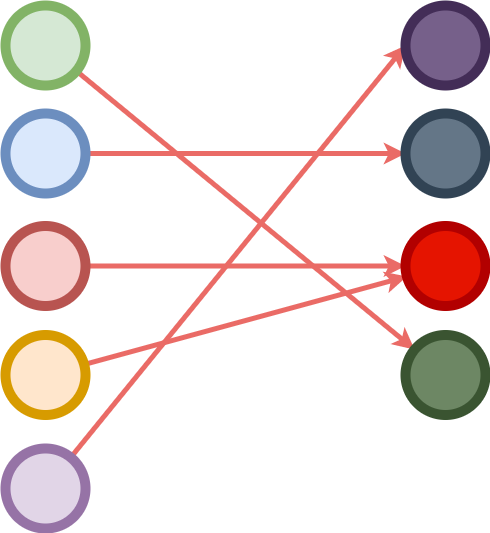
A function f : X → Y is surjective if \(∀ y ∈ Y, ∃ x ∈ X s.t. f(x) ==
y\). This states that for every element of Y, there should be at least one element of X such that
f(x) == y. So Y is an complete image of X.
-- Surjective : ∀ {a b} {A : Set a} {B : Set b} → (A → B) → Set (a ⊔ b)
-- Surjective f = ∀ y → ∃ λ x → f x ≡ y
record Surjection {f t} (From : Set f) (To : Set t) : Set (f ⊔ t) where
field
to : From → To
from : To → From
right-inverse-of : ∀ x → to (from x) ≡ x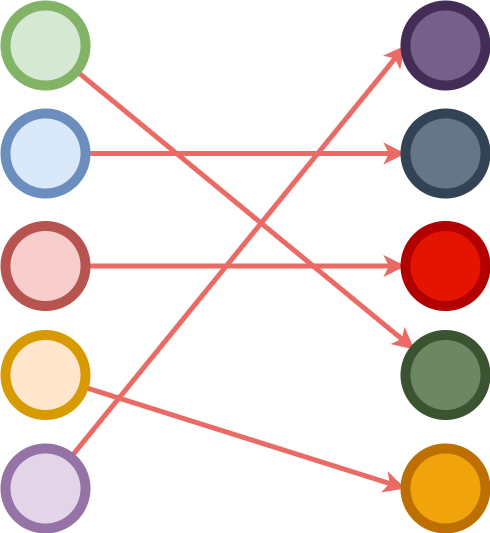
Bijection is the combination of injection and surjection. A bijection implies one-to-one correspondence from the domain to the codomain − each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. There are no unpaired elements.
record Bijection {f t} (From : Set f) (To : Set t) : Set (f ⊔ t) where
field
injection : Injection From To
surjection : Surjection From To